This post will guide you how to use Excel SEARCH function with syntax and examples in Microsoft excel.

Description

The Excel SEARCH function returns the number of the starting location of a substring in a text string. So you can use the SEARCH function to locate a text string within another text string and returns the position of the first character of find_text within text.

The SEARCH function is a build-in function in Microsoft Excel and it is categorized as a Text Function.

The SEARCH function is available in Excel 2016, Excel 2013, Excel 2010, Excel 2007, Excel 2003, Excel XP, Excel 2000, Excel 2011 for Mac.

Syntax

The syntax of the SEARCH function is as below:

= SEARCH (find_text, within_text,[start_num])

Where the SEARCH function arguments are:

• find_text -This is a required argument. The substring that you want to find
• within_text -This is a required argument. The text string in which you want to search for the substring (find_text).
• Start_num -This is an optional argument. The starting position to search.

Note:

• If find_text string is not found, the search function will return the #VALUE! Error value.
• If start_num value is omitted, it is set to be 1 by default.
• The SEARCH function is not case-sensitive.
• The SEARCH function support wildcard characters.

Excel SEARCH Function Examples

The below examples will show you how to use Excel SEARCH Text function to get the position of substring in a text string.

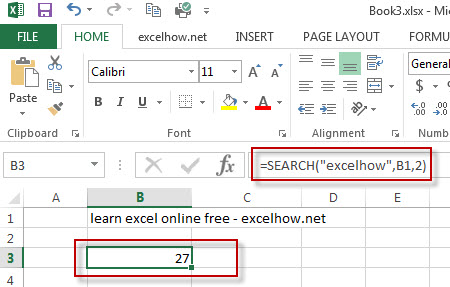
#1 To get the position of “excelhow” text string in B1 cell, starting at the second position, just using formula:= SEARCH(“excelhow”,B1,2).

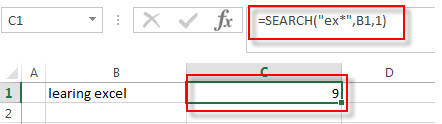
2# The search function use wildcard characters to look for a string starts with “ex”characters in cell B1, using the following formula:

Excel SEARCH Formula Examples

• Check If Cell Contains All Values from Range
  If you want to check if a cell contains all values in a list, you can use a combination of the SEARCH function, the SUMPRODUCT function, the ISNUMBER function and COUNTA function…
• Check if Cell Contains Certain Values but do not Contain Others Values
  Supposing that you have a list of text strings in the range B1:B3 and you need to check each Cell that if it contains one of several values in a range D2:D4 but do not contains any of values in range E2:E3….
• Get first match that cell contains one of several values in a range
  You can use a combination of the INDEX function, the MATCH function, the ISNUMBER function and the SEARCH function to create a new excel array formula to get first match cell contains…
• Get last match that cell contains one of several values in a range
  If you want to check a cell that if it contains one of several values in a range, you can use the SEARCH function to search find_text in a range inside a text string. Then we can use the LOOKUP function to get the last match values….
• Check if Cell contains one of many values from range
  Assuming that you have a list of text strings in the range B1:B3 and you want to check each text string if it contains one of several values in a range E1:E3. If it contains any of text string in range E1:E3, then it should be return TRUE value, otherwise, it should return FALSE….
• Extract Text between Brackets
  If you want to extract text between brackets in a cell, you need to create a formula based on the SEARCH function and the MID function….
• Extract Text between Parentheses
  If you want to extract text between parentheses in a cell, then you can use the search function within the MID function to create a new excel formula…
• Split Text String by Specified Character in Excel
  you can use the FIND function or SEARCH Function to get the position of the searched character within another string. Once you got the position number of the specified character, you can use the LEFT function to extract all the characters to the left of dash character (“-“)……
• The different between FIND and SEARCH functions
  There are two big differences between FIND and SEARCH functions in excel.The FIND function is case-sensitive. And the SEARCH function is case-insensitive.The FIND function is not allow to use wildcard. But the SEARCH function is allow to use wildcard characters…..
• Sort Cells by Specific word or words
  how to sort cells or text values in a column based on a specific word even if the word is in the text string in the cell. How do I sort cells in a column by the number of a specific word or words in excel……
• Insert The File Path and Filename into Cell
  If you want to insert a file path and filename into a cell in your current worksheet, you can use the CELL function to create a formual……..