This post will guide you how to Count the number of matches between two columns using a formula or vba code in Excel 2013/2016 or Excel office 365. How do I compare two columns within two different ranges or columns and count if the value in column1 found in column2 in Excel. You can use the SUMPRODUCT function to compare two columns, and is used to multiply the corresponding components in the given two ranges or arrays and returns the sum of those products.

1. Count Matches between Two Columns Using Formula

The Syntax of the SUMPRODUCS is as below:

=SUMPRODUCT(array1,[array2]…)

For Example, you have a data of list in both A2:A6 and B2:B6 and you wish to count any differences between those two ranges, and you can use the below SUMPRODUCT function:

=SUMPRODUCT(--(A2:A6=B2:B6))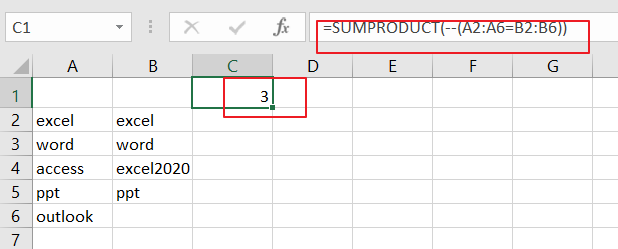

You can select cell C1 to place the final result, just click on it, and insert the above formula, then press Enter key.

Let’s See That How This Formula Works:

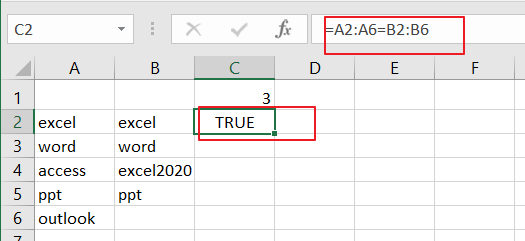
In the above example the expression A2:A6=B2:B6 will compare the value of those two ranges and generates an array result with TRUE and FALSE, like this:

{TRUE;TRUE;FALSE;TRUE;FALSE}

In the above example the expression A2:A6=B2:B6 will compare the value of those two ranges and generates an array result with TRUE and FALSE, like this:

{TRUE;TRUE;FALSE;TRUE;FALSE}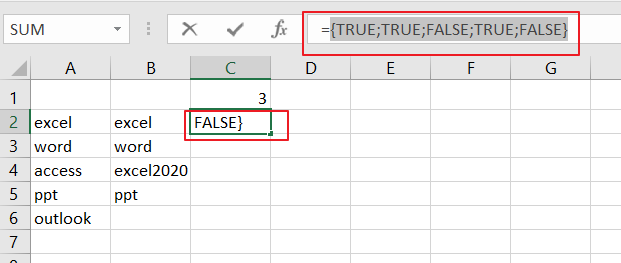

If cell values are equal and returns TRUE, otherwise returns FALSE.

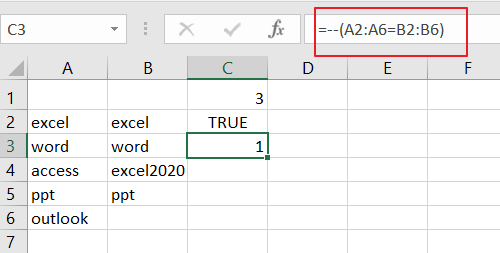
The double negative operator will convert the TRUE and FALSE value into 1 and 0 and return another array result like this:

{1;1;0;1;0}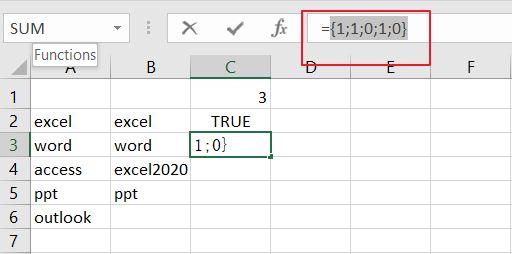

The SUMPRODUCT function will simply sum the values in the array and return the final result.

2. Count Matches between Two Columns Using VBA

Let’s see the second method, we’ll employ a User-Defined Function (UDF) written in VBA. This method offers flexibility and customization. Let’s explore how to set up and utilize the UDF.

Step1: Press Alt + F11 to open the Visual Basic for Applications (VBA) editor.

Step2:In the VBA editor, right-click on any item in the project explorer on the left.

Step3:Choose “Insert” and then “Module” to add a new module.

Step4:Copy the provided VBA code. Paste the code into the code window of the newly created module.

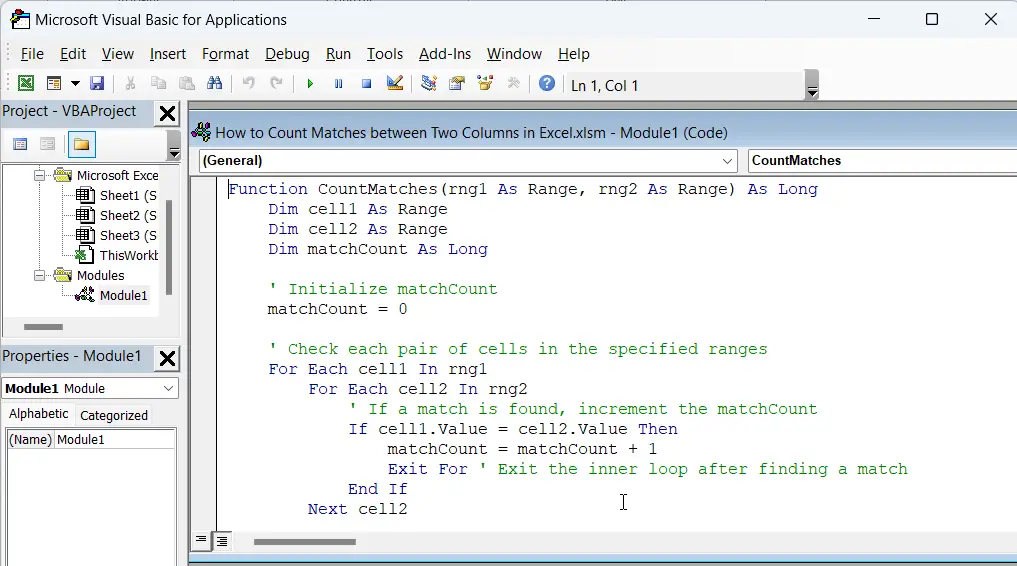
Function CountMatches(rng1 As Range, rng2 As Range) As Long
    Dim cell1 As Range
    Dim cell2 As Range
    Dim matchCount As Long
    
    ' Initialize matchCount
    matchCount = 0
    
    ' Check each pair of cells in the specified ranges
    For Each cell1 In rng1
        For Each cell2 In rng2
            ' If a match is found, increment the matchCount
            If cell1.Value = cell2.Value Then
                matchCount = matchCount + 1
                Exit For ' Exit the inner loop after finding a match
            End If
        Next cell2
    Next cell1
    
    ' Output the matchCount
    CountMatches = matchCount
End Function

Step5:Close the VBA editor by clicking the “X” button or pressing Alt + Q.

Step6: Go back to your Excel workbook. In any cell, type the following formula to use the newly created function:

=CountMatches(A2:A6, B2:B6)

Step7:Press Enter, and the result should be the count of matching values between columns A and B.

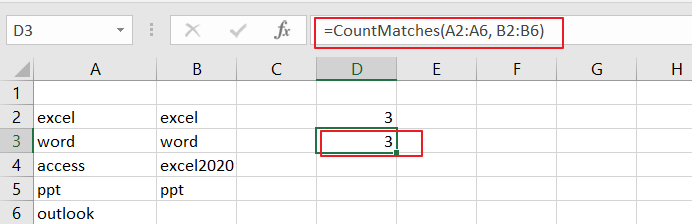
Now, you’ve successfully added and executed the VBA code to create a custom function for counting matches between two columns.

3. Video: Count Matches between Two Columns

This Excel Video tutorial, we’re diving into the art of counting matches between two columns using not one, but two powerful methods. We explore a formula-based approach and harness the flexibility of a User-Defined Function with VBA code in Excel 2013/2016/2019.

https://youtu.be/PJCOvPkJ1i4

4. Related Functions

• Excel SUMPRODUCT function
  The Excel SUMPRODUCT function multiplies corresponding components in the given one or more arrays or ranges, and returns the sum of those products. The syntax of the SUMPRODUCT function is as below:= SUMPRODUCT (array1,[array2],…)…