This post will guide you how to count the number of cells that are not equal to a specific value in a given range cells using a formula in Excel 2013/2016. Is there an easy way to count cells which are not equal to a particular value in your working data in Excel.
Table of Contents
1. Count Cells Not Equal to a Value Using Formula
Assuming that you want to count cells that not contain value defined in a selected range of cells or count cells that are not equal to a specific value. In this case, Excel has provided a simple solution to count cells that are not equal to a certain value. And you can use the COUNTIF function to solve this problem very easily. The below steps will show you how to count cells not equal to another value in Excel.
To Count the number of cells in range A2:A6 that are not equal to “excel” without case sensitive, you can use the below formula based on the COUNTIF function:
=COUNTIF(A2:A6,"<>excel")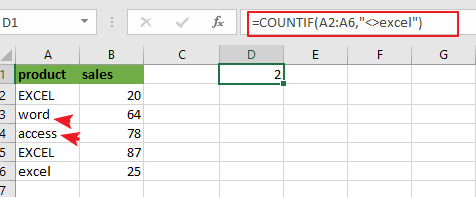
Let’s see how this formula works:
The COUNTIF function can be used to count the number of cells in a range that match the supplied criteria in Microsoft Excel. The range A2:A6 is the range of cells in which you want to match the criteria. The criteria “excel” is the value that you want to ignore during the count in the range “A2:A6”.
COUNTIF Function will count the number of cells in the range “A2:A6” that matches the condition you provide. And the “not equal to operator” will be used to count the cells in the range that does not equal to the value “excel”. And it will count all other values except this one.
The COUNTIF function is not case-sensitive. So if you wish to count cells exactly equal to a specific value, and you should use EXACT function.
Note: you can also use a value from a cell as its part of the criteria in the above COUNTIF function. To do this you need to use the ampersand operator to combine with that cell reference. Just like the below formula:
=COUNTIF(A2:A6,"<>"&A2)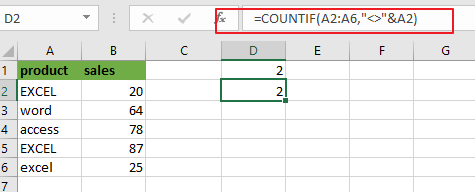
Note: the Cell A2 is the value that you want the cells not equal to in range A2:A6.
2. Count Cells Not Equal to a Specific Value Using VBA
Now, let’s explore a more advanced method using VBA code to achieve the same result. This approach provides greater flexibility and customization options for counting cells based on specific conditions. Follow these steps to implement the VBA solution in your Excel workbook.”
Press “Alt + F11” on your keyboard. This will open the Visual Basic for Applications (VBA) editor.
In the VBA editor window, right-click on any item in the Project Explorer pane
From the context menu, hover over “Insert” and then click on “Module.” This will insert a new module into your workbook’s VBA project.
Copy the provided VBA code. In the new module window, paste the copied code.
Sub CountNotEqual()
Dim rng As Range
Dim count As Long
' Prompt user to select the source range
On Error Resume Next
Set rng = Application.InputBox("Select the source range of cells:", Type:=8)
On Error GoTo 0
' Check if user canceled the prompt
If rng Is Nothing Then
MsgBox "Operation canceled.", vbExclamation
Exit Sub
End If
' Prompt user to enter the specific value
Dim specificValue As Variant
specificValue = InputBox("Enter the specific value to exclude:", "Specific Value")
' Check if user canceled the input box
If specificValue = "" Then
MsgBox "Operation canceled.", vbExclamation
Exit Sub
End If
' Count cells not equal to the specific value
For Each cell In rng
If cell.Value <> specificValue Then
count = count + 1
End If
Next cell
' Display the result
MsgBox "The count of cells not equal to '" & specificValue & "' is " & count
End Sub
Close the VBA editor window. Save your workbook to ensure that the VBA code is saved along with it. Switch back to the Excel workbook where you inserted the VBA code.
Press “Alt + F8” on your keyboard. This will open the “Macro” dialog box.
In the “Macro” dialog box, you should see the macro named “CountNotEqual.”
Select “CountNotEqual” from the list of macros. Click the “Run” button.
After running the macro, a prompt dialog will appear asking you to select the source range of cells.
Click and drag to select the range of cells you want to count. Alternatively, you can click on the first cell of the range and then hold down the Shift key while clicking on the last cell of the range.
Once you’ve selected the range, click “OK.”
After selecting the range, another prompt dialog will appear asking you to enter the specific value that you want to exclude from the count.
Type the specific value into the input box. Click “OK.”
The macro will count the cells in the selected range that are not equal to the specified value.
The result will be displayed in a message box. Click “OK” on the message box to close it.
3. Video: Count Cells Not Equal to a Specific Value
This Excel video tutorial, we’ll explore two methods to count cells not equal to a specific value. We’ll start with a formula-based approach using the COUNTIF function, followed by a VBA method for more advanced users.
4. Related Functions
- Excel COUNTIF function
The Excel COUNTIF function will count the number of cells in a range that meet a given criteria. This function can be used to count the different kinds of cells with number, date, text values, blank, non-blanks, or containing specific characters.etc.= COUNTIF (range, criteria)… - Excel EXACT function
The Excel EXACT function compares if two text strings are the same and returns TRUE if they are the same, Or, it will return FALSE.The syntax of the EXACT function is as below:= EXACT (text1,text2)…