If you want to split a number with more than one digits into each individual digit in each column, what you can do? I think you can use the combination of MID and COLUMN functions to resolve your issue. Please see the method below in this article.

Let’s study the two functions first.

#1 MID function is used for capturing a specified length of characters from a string.

The formula is = MID(text, start_num, num_chars).

#2 COLUMN function is used for returning the column number refer to the entering reference.

The formula is = COLUMN(reference)

COLUMN() without any reference returns the current column number for the selected cell. See example below.

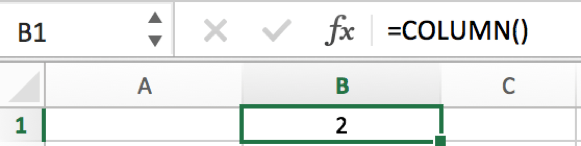
Then we can start to learn how can we split a number into each individual digit.

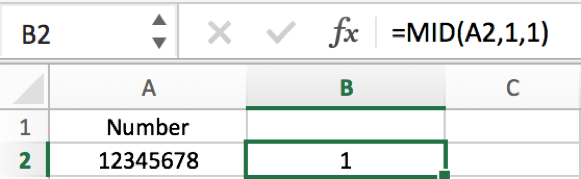
#1 First, prepare a number like 12345678. We can try to cut the first digit from this number. Enter =MID(A2,1,1) in B2 for example. A2 is the cell for number, 1 is the start position, 1 is the length of digit. We get the result below.

#2 For MID function, the second parameter ‘start_num’, we can use COLUMN function to replace manual entering the start position. For example, we can enter =MID(A2,COLUMN(),1) in B2 to get the split digit.

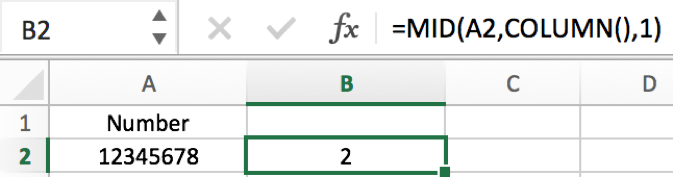
Verify that we get the returned value 2. That’s because COLUMN() returns the current column number, and the selected cell is B2, so the MID function equals to =MID(A2,2,1), so the returned value is 2.

 

#3 If we want to get eight individual digits from number 12345678 and put them into column B2 to I2. How can we do it? In above sample we can know COLUMN() returns 2 for B2, so if we want to get the first digit from number 12345678 into B2, we need to get return value 1, so we can use COLUMN()-1 as start number criteria.

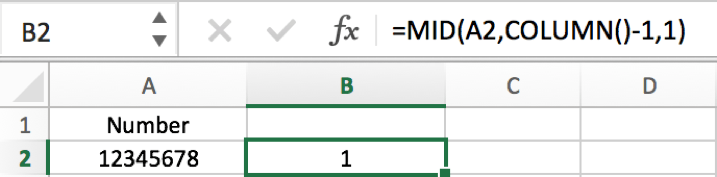
#4 In cell C2 we need to get the second individual digit from number in A2, so we add $ before A2 in formula =MID($A2,COLUMN()-1,1), in this case we can directly drag B2 and use this formula to fill C2:I2.

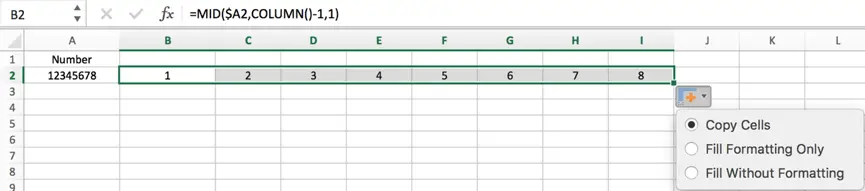
Notes, if we still use formula =MID(A2,COLUMN()-1,1) without $ before A2, in C2 the formula will change to =MID(B2,COLUMN()-1,1) improperly.