This post will guide you how to use Excel XIRR function with syntax and examples in Microsoft excel.

Description

The Excel XIRR function returns the internal rate of return for a series of cash flows that is not necessarily periodic. And if you want to get the internal rate of return for a series of periodic cash flows, you can use the IRR function in Excel.

The XIRR function is a build-in function in Microsoft Excel and it is categorized as a Financial Function.

The XIRR function is available in Excel 2016, Excel 2013, Excel 2010, Excel 2007, Excel 2011 for Mac.

Syntax

The syntax of the XIRR function is as below:

= XIRR (values, dates, [guess])

Where the XIRR function arguments are:

• Values -This is a required argument. An array or cell reference that contain numbers for which you want to calculate the internal rate of return. And the values must include at least one positive value and one negative value.
• Dates -This is a required argument. A series of dates that corresponds to the cash flow payments.
• Guess – This is an optional argument. An initial guess at the internal rate of return. If it is omitted, and it will be set as 0.1 or 10%.

Note:

• The values arguments must contain at least one positive value and one negative cash flow value, or the XIRR function will return the #NUM! Error.
• If you provide an invalid date in the date argument, the XIRR function will return the #NUM! Error.

Excel XIRR Function Examples

The below examples will show you how to use Excel XIRR Function to calculate the internal rate of return for a series of cash flows.

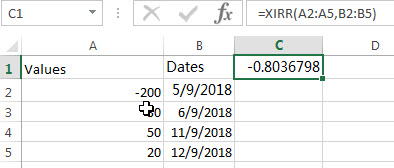
#1 to get the internal rate of return, using the following formula:

=XIRR(A2:A5,B2:B5)

---

Related Functions

• Excel IRR Function
  The Excel IRR function returns the internal rate of return for a series of cash flows and the cash flows must be occurred at regular intervals (monthly or annually).The syntax of the IRR function is as below:=IRR(values, [guess])…

Related Examples

• Calculate Stock Rate of Return
  You can try to calculate the rate of return by manually, or you use an Excel formula to achieve the result. The best way to calculate your rate of return is to use the EXCEL XIRR function,…