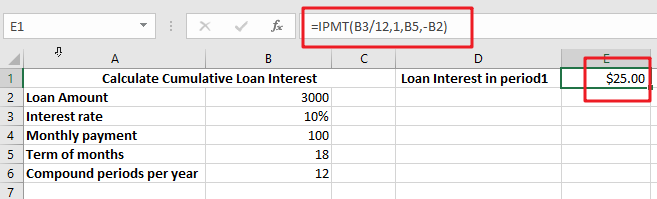
Using the IPMT function in Excel, we can compute the interest payment on any loan. This step-by-step tutorial will guide Excel users of all skill levels through the process to calculate interest for given period.
Finally, the formula:
=IPMT(B3/12,1,B5,-B2)
Table of Contents
The IPMT Function’s Syntax
IPMT reimburses the interest paid on any investment or loan for a certain term.
=IPMT(rate, per, nper, pv, [fv], [type])
IMPT – The interest excel IMPT function is used to compute the interest component of a loan payment over a specified payment term.
Rate — This metric is used to denote the interest rate.
Period — This is the time frame in which we want to work.
The comma sign (,) is used to denote a separator in a list of values.
Parenthesis () – This symbol is primarily used to group elements.
How Interest on Interest Is Calculated
Interest on interest works by paying interest on both previous interest payments and the starting amount of capital invested or saved.
For example, United States savings bonds are financial instruments that pay investors interest on interest, compounded semi-annually and accruing monthly for 30 years. The majority of bank savings accounts also pay interest on interest, with payments compounded monthly.
Interest on interest is not the same thing as plain interest. Simple interest is charged solely on the initial principal amount, while interest on interest is levied on the main amount of the bond or loan plus any previously accumulated interest.
Interest on Interest Calculation
When compound interest is used to calculate interest on interest, the compound interest formula is used to compute the amount of accrued interest on the principal invested or borrowed. Compound interest on a loan or deposit is calculated using the principal amount, the yearly interest rate, and the number of compounding periods.
Compound interest is calculated by adding 1 to the interest rate in decimal notation, multiplying by the total number of compound periods, and multiplying by the principal amount. Subtract the original principal amount from the resultant value.
I=[P(1 + I ) n ]
−P
I=Interest compounded
P=Principal
i=Periodic nominal interest rate
n denotes the number of compounding periods.
Where:
P stands for principal.
I = nominal annual interest rate expressed as a percentage
n denotes the total number of compounding periods.
The “rule of 72” calculates the number of years required for an investment or savings to double in value when interest on interest is compounded. Divide 72 by the interest rate to get an approximation of the number of years.
Example
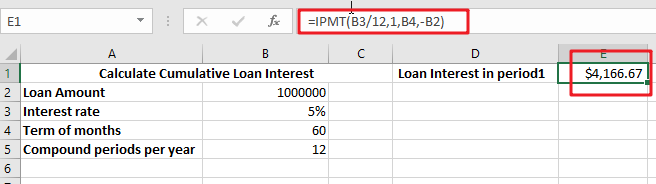
As an example, consider calculating the compound interest on a $1 million deposit. Annually, the principal is compounded at a rate of 5%. Five compounding periods are used in total, each representing a one-year term.
Consider calculating the compound interest on a $1 million deposit. However, this deposit is compounded on a monthly basis. The yearly interest rate is 5%, and interest is compounded annually for five years.
Divide the yearly interest rate by 12 months to get the monthly interest rate. The monthly interest rate as a consequence is 0.417 percent. Calculate the total number of periods by multiplying the number of years by 12 months, as interest compounds monthly. The total number of periods in this situation is 60, or 5 years x 12 months.
Related Functions
- Excel IPMT function
The Excel IPMT function used to calculate the interest payment for an investment based on a constant payment schedule and a constant interest rage.The syntax of the IPMT function is as below:= IPMT (rate, per, nper, pv, [fv], [type])….